Masked image modeling with Autoencoders
Author: Aritra Roy Gosthipaty, Sayak Paul
Date created: 2021/12/20
Last modified: 2021/12/21
Description: Implementing Masked Autoencoders for self-supervised pretraining.
Introduction
In deep learning, models with growing capacity and capability can easily overfit on large datasets (ImageNet-1K). In the field of natural language processing, the appetite for data has been successfully addressed by self-supervised pretraining.
In the academic paper Masked Autoencoders Are Scalable Vision Learners by He et. al. the authors propose a simple yet effective method to pretrain large vision models (here ViT Huge). Inspired from the pretraining algorithm of BERT (Devlin et al.), they mask patches of an image and, through an autoencoder predict the masked patches. In the spirit of "masked language modeling", this pretraining task could be referred to as "masked image modeling".
In this example, we implement Masked Autoencoders Are Scalable Vision Learners with the CIFAR-10 dataset. After pretraining a scaled down version of ViT, we also implement the linear evaluation pipeline on CIFAR-10.
This implementation covers (MAE refers to Masked Autoencoder):
- The masking algorithm
- MAE encoder
- MAE decoder
- Evaluation with linear probing
As a reference, we reuse some of the code presented in this example.
Imports
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import tensorflow as tf
import keras
from keras import layers
import matplotlib.pyplot as plt
import numpy as np
import random
# Setting seeds for reproducibility.
SEED = 42
keras.utils.set_random_seed(SEED)
Hyperparameters for pretraining
Please feel free to change the hyperparameters and check your results. The best way to get an intuition about the architecture is to experiment with it. Our hyperparameters are heavily inspired by the design guidelines laid out by the authors in the original paper.
# DATA
BUFFER_SIZE = 1024
BATCH_SIZE = 256
AUTO = tf.data.AUTOTUNE
INPUT_SHAPE = (32, 32, 3)
NUM_CLASSES = 10
# OPTIMIZER
LEARNING_RATE = 5e-3
WEIGHT_DECAY = 1e-4
# PRETRAINING
EPOCHS = 100
# AUGMENTATION
IMAGE_SIZE = 48 # We will resize input images to this size.
PATCH_SIZE = 6 # Size of the patches to be extracted from the input images.
NUM_PATCHES = (IMAGE_SIZE // PATCH_SIZE) ** 2
MASK_PROPORTION = 0.75 # We have found 75% masking to give us the best results.
# ENCODER and DECODER
LAYER_NORM_EPS = 1e-6
ENC_PROJECTION_DIM = 128
DEC_PROJECTION_DIM = 64
ENC_NUM_HEADS = 4
ENC_LAYERS = 6
DEC_NUM_HEADS = 4
DEC_LAYERS = (
2 # The decoder is lightweight but should be reasonably deep for reconstruction.
)
ENC_TRANSFORMER_UNITS = [
ENC_PROJECTION_DIM * 2,
ENC_PROJECTION_DIM,
] # Size of the transformer layers.
DEC_TRANSFORMER_UNITS = [
DEC_PROJECTION_DIM * 2,
DEC_PROJECTION_DIM,
]
Load and prepare the CIFAR-10 dataset
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
(x_train, y_train), (x_val, y_val) = (
(x_train[:40000], y_train[:40000]),
(x_train[40000:], y_train[40000:]),
)
print(f"Training samples: {len(x_train)}")
print(f"Validation samples: {len(x_val)}")
print(f"Testing samples: {len(x_test)}")
train_ds = tf.data.Dataset.from_tensor_slices(x_train)
train_ds = train_ds.shuffle(BUFFER_SIZE).batch(BATCH_SIZE).prefetch(AUTO)
val_ds = tf.data.Dataset.from_tensor_slices(x_val)
val_ds = val_ds.batch(BATCH_SIZE).prefetch(AUTO)
test_ds = tf.data.Dataset.from_tensor_slices(x_test)
test_ds = test_ds.batch(BATCH_SIZE).prefetch(AUTO)
Training samples: 40000
Validation samples: 10000
Testing samples: 10000
Data augmentation
In previous self-supervised pretraining methodologies (SimCLR alike), we have noticed that the data augmentation pipeline plays an important role. On the other hand the authors of this paper point out that Masked Autoencoders do not rely on augmentations. They propose a simple augmentation pipeline of:
- Resizing
- Random cropping (fixed-sized or random sized)
- Random horizontal flipping
def get_train_augmentation_model():
model = keras.Sequential(
[
layers.Rescaling(1 / 255.0),
layers.Resizing(INPUT_SHAPE[0] + 20, INPUT_SHAPE[0] + 20),
layers.RandomCrop(IMAGE_SIZE, IMAGE_SIZE),
layers.RandomFlip("horizontal"),
],
name="train_data_augmentation",
)
return model
def get_test_augmentation_model():
model = keras.Sequential(
[
layers.Rescaling(1 / 255.0),
layers.Resizing(IMAGE_SIZE, IMAGE_SIZE),
],
name="test_data_augmentation",
)
return model
A layer for extracting patches from images
This layer takes images as input and divides them into patches. The layer also includes two utility method:
show_patched_image– Takes a batch of images and its corresponding patches to plot a random pair of image and patches.reconstruct_from_patch– Takes a single instance of patches and stitches them together into the original image.
class Patches(layers.Layer):
def __init__(self, patch_size=PATCH_SIZE, **kwargs):
super().__init__(**kwargs)
self.patch_size = patch_size
# Assuming the image has three channels each patch would be
# of size (patch_size, patch_size, 3).
self.resize = layers.Reshape((-1, patch_size * patch_size * 3))
def call(self, images):
# Create patches from the input images
patches = tf.image.extract_patches(
images=images,
sizes=[1, self.patch_size, self.patch_size, 1],
strides=[1, self.patch_size, self.patch_size, 1],
rates=[1, 1, 1, 1],
padding="VALID",
)
# Reshape the patches to (batch, num_patches, patch_area) and return it.
patches = self.resize(patches)
return patches
def show_patched_image(self, images, patches):
# This is a utility function which accepts a batch of images and its
# corresponding patches and help visualize one image and its patches
# side by side.
idx = np.random.choice(patches.shape[0])
print(f"Index selected: {idx}.")
plt.figure(figsize=(4, 4))
plt.imshow(keras.utils.array_to_img(images[idx]))
plt.axis("off")
plt.show()
n = int(np.sqrt(patches.shape[1]))
plt.figure(figsize=(4, 4))
for i, patch in enumerate(patches[idx]):
ax = plt.subplot(n, n, i + 1)
patch_img = tf.reshape(patch, (self.patch_size, self.patch_size, 3))
plt.imshow(keras.utils.img_to_array(patch_img))
plt.axis("off")
plt.show()
# Return the index chosen to validate it outside the method.
return idx
# taken from https://stackoverflow.com/a/58082878/10319735
def reconstruct_from_patch(self, patch):
# This utility function takes patches from a *single* image and
# reconstructs it back into the image. This is useful for the train
# monitor callback.
num_patches = patch.shape[0]
n = int(np.sqrt(num_patches))
patch = tf.reshape(patch, (num_patches, self.patch_size, self.patch_size, 3))
rows = tf.split(patch, n, axis=0)
rows = [tf.concat(tf.unstack(x), axis=1) for x in rows]
reconstructed = tf.concat(rows, axis=0)
return reconstructed
Let's visualize the image patches.
# Get a batch of images.
image_batch = next(iter(train_ds))
# Augment the images.
augmentation_model = get_train_augmentation_model()
augmented_images = augmentation_model(image_batch)
# Define the patch layer.
patch_layer = Patches()
# Get the patches from the batched images.
patches = patch_layer(images=augmented_images)
# Now pass the images and the corresponding patches
# to the `show_patched_image` method.
random_index = patch_layer.show_patched_image(images=augmented_images, patches=patches)
# Chose the same chose image and try reconstructing the patches
# into the original image.
image = patch_layer.reconstruct_from_patch(patches[random_index])
plt.imshow(image)
plt.axis("off")
plt.show()
Index selected: 102.



Patch encoding with masking
Quoting the paper
Following ViT, we divide an image into regular non-overlapping patches. Then we sample a subset of patches and mask (i.e., remove) the remaining ones. Our sampling strategy is straightforward: we sample random patches without replacement, following a uniform distribution. We simply refer to this as “random sampling”.
This layer includes masking and encoding the patches.
The utility methods of the layer are:
get_random_indices– Provides the mask and unmask indices.generate_masked_image– Takes patches and unmask indices, results in a random masked image. This is an essential utility method for our training monitor callback (defined later).
class PatchEncoder(layers.Layer):
def __init__(
self,
patch_size=PATCH_SIZE,
projection_dim=ENC_PROJECTION_DIM,
mask_proportion=MASK_PROPORTION,
downstream=False,
**kwargs,
):
super().__init__(**kwargs)
self.patch_size = patch_size
self.projection_dim = projection_dim
self.mask_proportion = mask_proportion
self.downstream = downstream
# This is a trainable mask token initialized randomly from a normal
# distribution.
self.mask_token = tf.Variable(
tf.random.normal([1, patch_size * patch_size * 3]), trainable=True
)
def build(self, input_shape):
(_, self.num_patches, self.patch_area) = input_shape
# Create the projection layer for the patches.
self.projection = layers.Dense(units=self.projection_dim)
# Create the positional embedding layer.
self.position_embedding = layers.Embedding(
input_dim=self.num_patches, output_dim=self.projection_dim
)
# Number of patches that will be masked.
self.num_mask = int(self.mask_proportion * self.num_patches)
def call(self, patches):
# Get the positional embeddings.
batch_size = tf.shape(patches)[0]
positions = tf.range(start=0, limit=self.num_patches, delta=1)
pos_embeddings = self.position_embedding(positions[tf.newaxis, ...])
pos_embeddings = tf.tile(
pos_embeddings, [batch_size, 1, 1]
) # (B, num_patches, projection_dim)
# Embed the patches.
patch_embeddings = (
self.projection(patches) + pos_embeddings
) # (B, num_patches, projection_dim)
if self.downstream:
return patch_embeddings
else:
mask_indices, unmask_indices = self.get_random_indices(batch_size)
# The encoder input is the unmasked patch embeddings. Here we gather
# all the patches that should be unmasked.
unmasked_embeddings = tf.gather(
patch_embeddings, unmask_indices, axis=1, batch_dims=1
) # (B, unmask_numbers, projection_dim)
# Get the unmasked and masked position embeddings. We will need them
# for the decoder.
unmasked_positions = tf.gather(
pos_embeddings, unmask_indices, axis=1, batch_dims=1
) # (B, unmask_numbers, projection_dim)
masked_positions = tf.gather(
pos_embeddings, mask_indices, axis=1, batch_dims=1
) # (B, mask_numbers, projection_dim)
# Repeat the mask token number of mask times.
# Mask tokens replace the masks of the image.
mask_tokens = tf.repeat(self.mask_token, repeats=self.num_mask, axis=0)
mask_tokens = tf.repeat(
mask_tokens[tf.newaxis, ...], repeats=batch_size, axis=0
)
# Get the masked embeddings for the tokens.
masked_embeddings = self.projection(mask_tokens) + masked_positions
return (
unmasked_embeddings, # Input to the encoder.
masked_embeddings, # First part of input to the decoder.
unmasked_positions, # Added to the encoder outputs.
mask_indices, # The indices that were masked.
unmask_indices, # The indices that were unmaksed.
)
def get_random_indices(self, batch_size):
# Create random indices from a uniform distribution and then split
# it into mask and unmask indices.
rand_indices = tf.argsort(
tf.random.uniform(shape=(batch_size, self.num_patches)), axis=-1
)
mask_indices = rand_indices[:, : self.num_mask]
unmask_indices = rand_indices[:, self.num_mask :]
return mask_indices, unmask_indices
def generate_masked_image(self, patches, unmask_indices):
# Choose a random patch and it corresponding unmask index.
idx = np.random.choice(patches.shape[0])
patch = patches[idx]
unmask_index = unmask_indices[idx]
# Build a numpy array of same shape as patch.
new_patch = np.zeros_like(patch)
# Iterate of the new_patch and plug the unmasked patches.
count = 0
for i in range(unmask_index.shape[0]):
new_patch[unmask_index[i]] = patch[unmask_index[i]]
return new_patch, idx
Let's see the masking process in action on a sample image.
# Create the patch encoder layer.
patch_encoder = PatchEncoder()
# Get the embeddings and positions.
(
unmasked_embeddings,
masked_embeddings,
unmasked_positions,
mask_indices,
unmask_indices,
) = patch_encoder(patches=patches)
# Show a maksed patch image.
new_patch, random_index = patch_encoder.generate_masked_image(patches, unmask_indices)
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
img = patch_layer.reconstruct_from_patch(new_patch)
plt.imshow(keras.utils.array_to_img(img))
plt.axis("off")
plt.title("Masked")
plt.subplot(1, 2, 2)
img = augmented_images[random_index]
plt.imshow(keras.utils.array_to_img(img))
plt.axis("off")
plt.title("Original")
plt.show()

MLP
This serves as the fully connected feed forward network of the transformer architecture.
def mlp(x, dropout_rate, hidden_units):
for units in hidden_units:
x = layers.Dense(units, activation=tf.nn.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x
MAE encoder
The MAE encoder is ViT. The only point to note here is that the encoder outputs a layer normalized output.
def create_encoder(num_heads=ENC_NUM_HEADS, num_layers=ENC_LAYERS):
inputs = layers.Input((None, ENC_PROJECTION_DIM))
x = inputs
for _ in range(num_layers):
# Layer normalization 1.
x1 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
# Create a multi-head attention layer.
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=ENC_PROJECTION_DIM, dropout=0.1
)(x1, x1)
# Skip connection 1.
x2 = layers.Add()([attention_output, x])
# Layer normalization 2.
x3 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x2)
# MLP.
x3 = mlp(x3, hidden_units=ENC_TRANSFORMER_UNITS, dropout_rate=0.1)
# Skip connection 2.
x = layers.Add()([x3, x2])
outputs = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
return keras.Model(inputs, outputs, name="mae_encoder")
MAE decoder
The authors point out that they use an asymmetric autoencoder model. They use a lightweight decoder that takes "<10% computation per token vs. the encoder". We are not specific with the "<10% computation" in our implementation but have used a smaller decoder (both in terms of depth and projection dimensions).
def create_decoder(
num_layers=DEC_LAYERS, num_heads=DEC_NUM_HEADS, image_size=IMAGE_SIZE
):
inputs = layers.Input((NUM_PATCHES, ENC_PROJECTION_DIM))
x = layers.Dense(DEC_PROJECTION_DIM)(inputs)
for _ in range(num_layers):
# Layer normalization 1.
x1 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
# Create a multi-head attention layer.
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=DEC_PROJECTION_DIM, dropout=0.1
)(x1, x1)
# Skip connection 1.
x2 = layers.Add()([attention_output, x])
# Layer normalization 2.
x3 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x2)
# MLP.
x3 = mlp(x3, hidden_units=DEC_TRANSFORMER_UNITS, dropout_rate=0.1)
# Skip connection 2.
x = layers.Add()([x3, x2])
x = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x)
x = layers.Flatten()(x)
pre_final = layers.Dense(units=image_size * image_size * 3, activation="sigmoid")(x)
outputs = layers.Reshape((image_size, image_size, 3))(pre_final)
return keras.Model(inputs, outputs, name="mae_decoder")
MAE trainer
This is the trainer module. We wrap the encoder and decoder inside of a tf.keras.Model
subclass. This allows us to customize what happens in the model.fit() loop.
class MaskedAutoencoder(keras.Model):
def __init__(
self,
train_augmentation_model,
test_augmentation_model,
patch_layer,
patch_encoder,
encoder,
decoder,
**kwargs,
):
super().__init__(**kwargs)
self.train_augmentation_model = train_augmentation_model
self.test_augmentation_model = test_augmentation_model
self.patch_layer = patch_layer
self.patch_encoder = patch_encoder
self.encoder = encoder
self.decoder = decoder
def calculate_loss(self, images, test=False):
# Augment the input images.
if test:
augmented_images = self.test_augmentation_model(images)
else:
augmented_images = self.train_augmentation_model(images)
# Patch the augmented images.
patches = self.patch_layer(augmented_images)
# Encode the patches.
(
unmasked_embeddings,
masked_embeddings,
unmasked_positions,
mask_indices,
unmask_indices,
) = self.patch_encoder(patches)
# Pass the unmaksed patche to the encoder.
encoder_outputs = self.encoder(unmasked_embeddings)
# Create the decoder inputs.
encoder_outputs = encoder_outputs + unmasked_positions
decoder_inputs = tf.concat([encoder_outputs, masked_embeddings], axis=1)
# Decode the inputs.
decoder_outputs = self.decoder(decoder_inputs)
decoder_patches = self.patch_layer(decoder_outputs)
loss_patch = tf.gather(patches, mask_indices, axis=1, batch_dims=1)
loss_output = tf.gather(decoder_patches, mask_indices, axis=1, batch_dims=1)
# Compute the total loss.
total_loss = self.compute_loss(y=loss_patch, y_pred=loss_output)
return total_loss, loss_patch, loss_output
def train_step(self, images):
with tf.GradientTape() as tape:
total_loss, loss_patch, loss_output = self.calculate_loss(images)
# Apply gradients.
train_vars = [
self.train_augmentation_model.trainable_variables,
self.patch_layer.trainable_variables,
self.patch_encoder.trainable_variables,
self.encoder.trainable_variables,
self.decoder.trainable_variables,
]
grads = tape.gradient(total_loss, train_vars)
tv_list = []
for grad, var in zip(grads, train_vars):
for g, v in zip(grad, var):
tv_list.append((g, v))
self.optimizer.apply_gradients(tv_list)
# Report progress.
results = {}
for metric in self.metrics:
metric.update_state(loss_patch, loss_output)
results[metric.name] = metric.result()
return results
def test_step(self, images):
total_loss, loss_patch, loss_output = self.calculate_loss(images, test=True)
# Update the trackers.
results = {}
for metric in self.metrics:
metric.update_state(loss_patch, loss_output)
results[metric.name] = metric.result()
return results
Model initialization
train_augmentation_model = get_train_augmentation_model()
test_augmentation_model = get_test_augmentation_model()
patch_layer = Patches()
patch_encoder = PatchEncoder()
encoder = create_encoder()
decoder = create_decoder()
mae_model = MaskedAutoencoder(
train_augmentation_model=train_augmentation_model,
test_augmentation_model=test_augmentation_model,
patch_layer=patch_layer,
patch_encoder=patch_encoder,
encoder=encoder,
decoder=decoder,
)
Training callbacks
Visualization callback
# Taking a batch of test inputs to measure model's progress.
test_images = next(iter(test_ds))
class TrainMonitor(keras.callbacks.Callback):
def __init__(self, epoch_interval=None):
self.epoch_interval = epoch_interval
def on_epoch_end(self, epoch, logs=None):
if self.epoch_interval and epoch % self.epoch_interval == 0:
test_augmented_images = self.model.test_augmentation_model(test_images)
test_patches = self.model.patch_layer(test_augmented_images)
(
test_unmasked_embeddings,
test_masked_embeddings,
test_unmasked_positions,
test_mask_indices,
test_unmask_indices,
) = self.model.patch_encoder(test_patches)
test_encoder_outputs = self.model.encoder(test_unmasked_embeddings)
test_encoder_outputs = test_encoder_outputs + test_unmasked_positions
test_decoder_inputs = tf.concat(
[test_encoder_outputs, test_masked_embeddings], axis=1
)
test_decoder_outputs = self.model.decoder(test_decoder_inputs)
# Show a maksed patch image.
test_masked_patch, idx = self.model.patch_encoder.generate_masked_image(
test_patches, test_unmask_indices
)
print(f"\nIdx chosen: {idx}")
original_image = test_augmented_images[idx]
masked_image = self.model.patch_layer.reconstruct_from_patch(
test_masked_patch
)
reconstructed_image = test_decoder_outputs[idx]
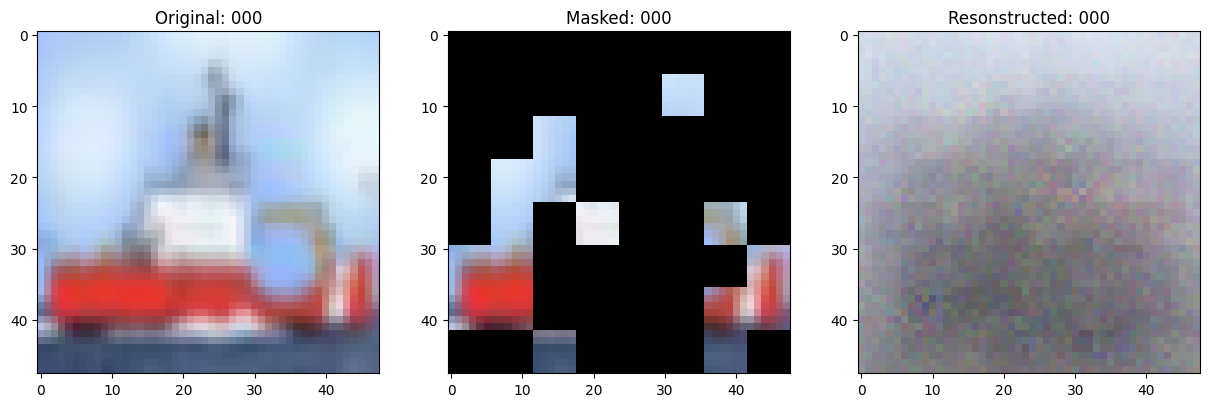
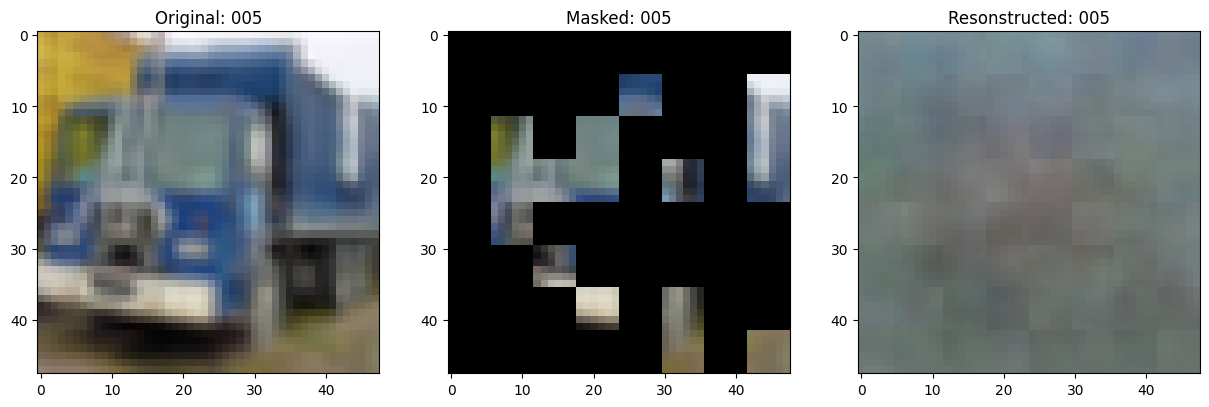
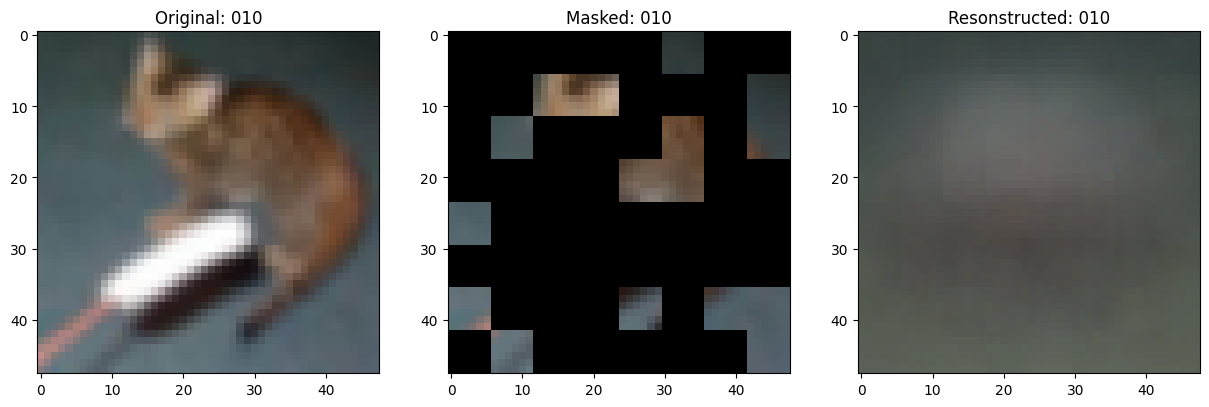
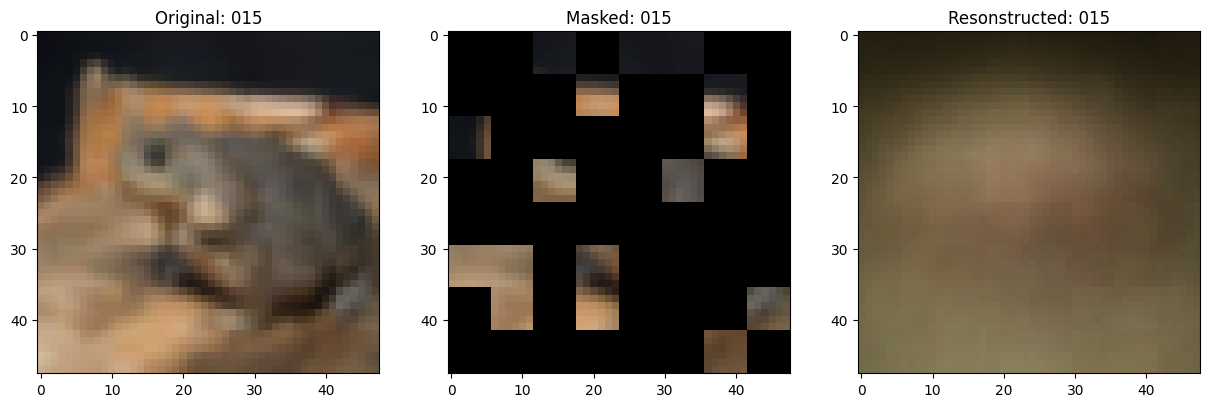
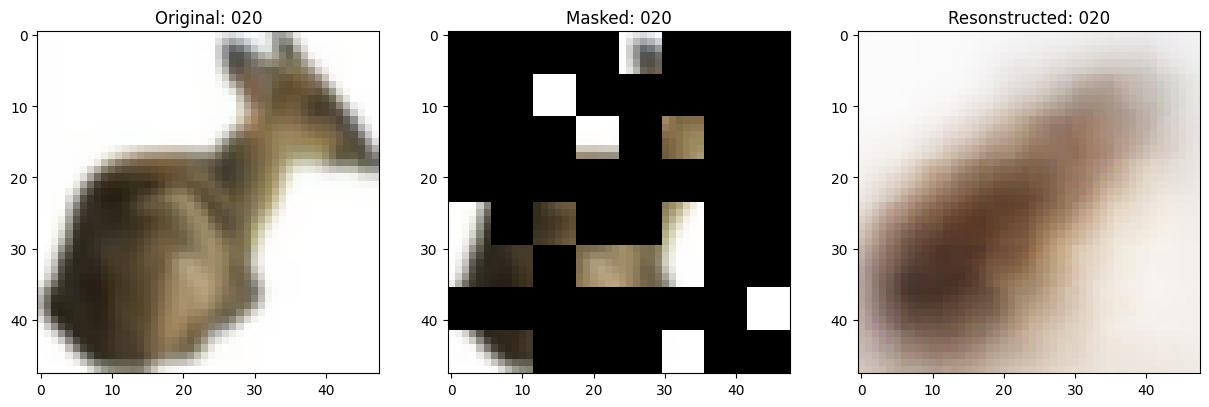
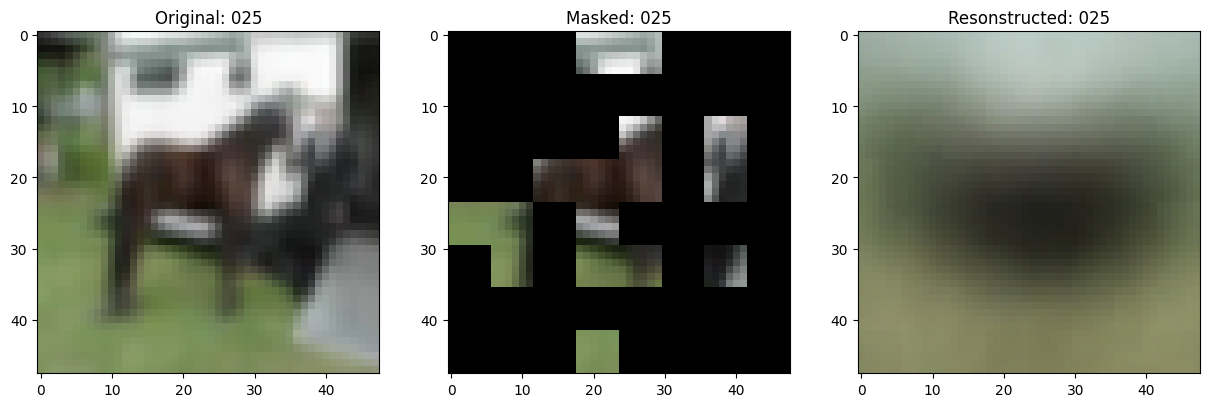
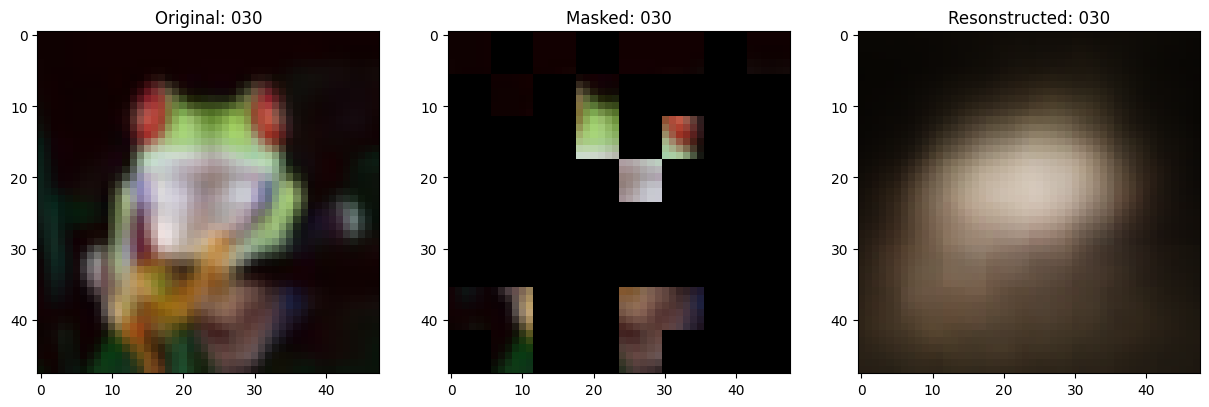
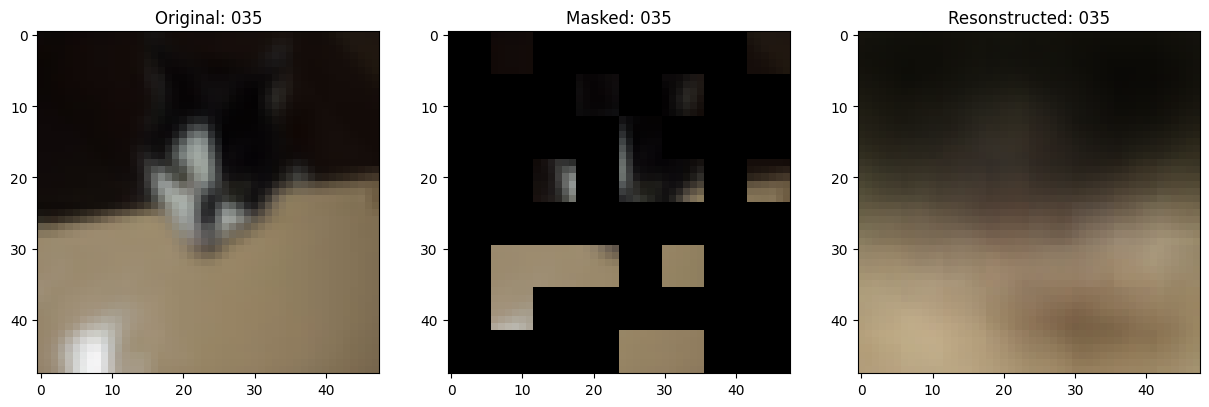
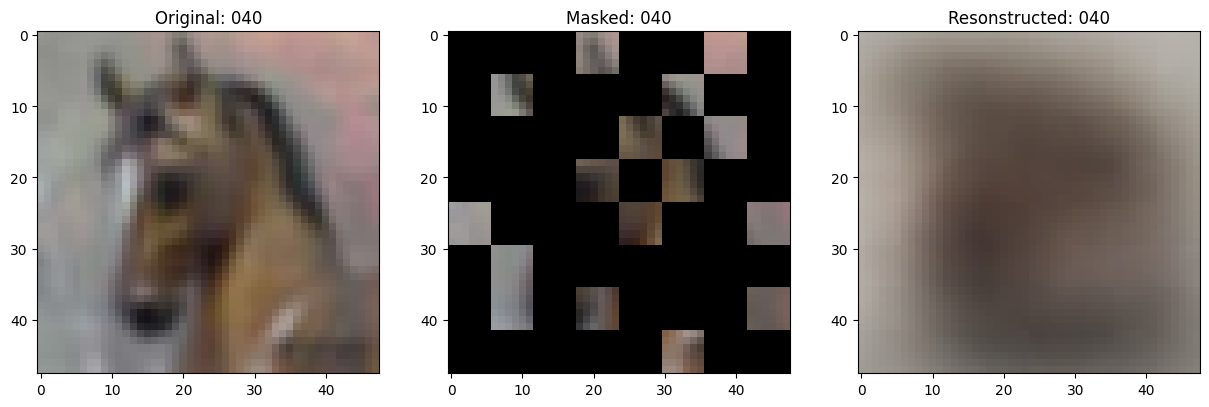
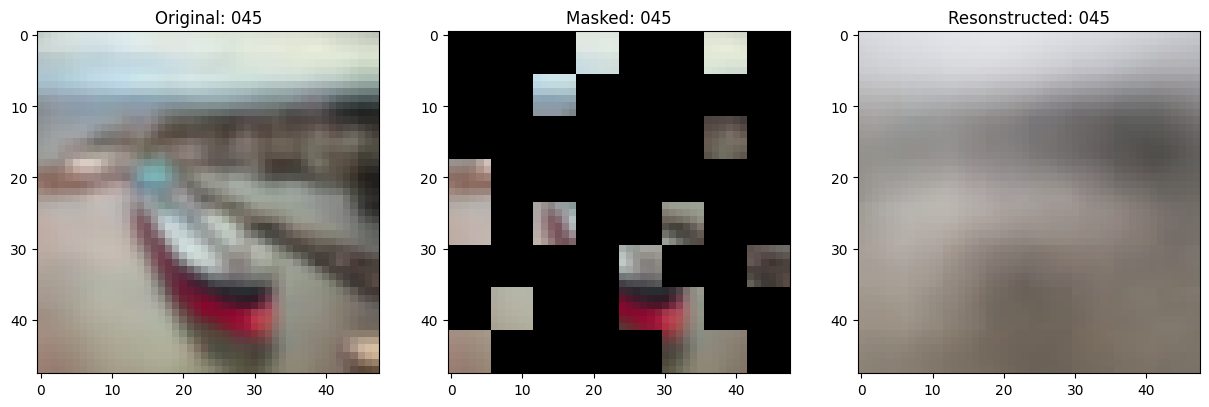
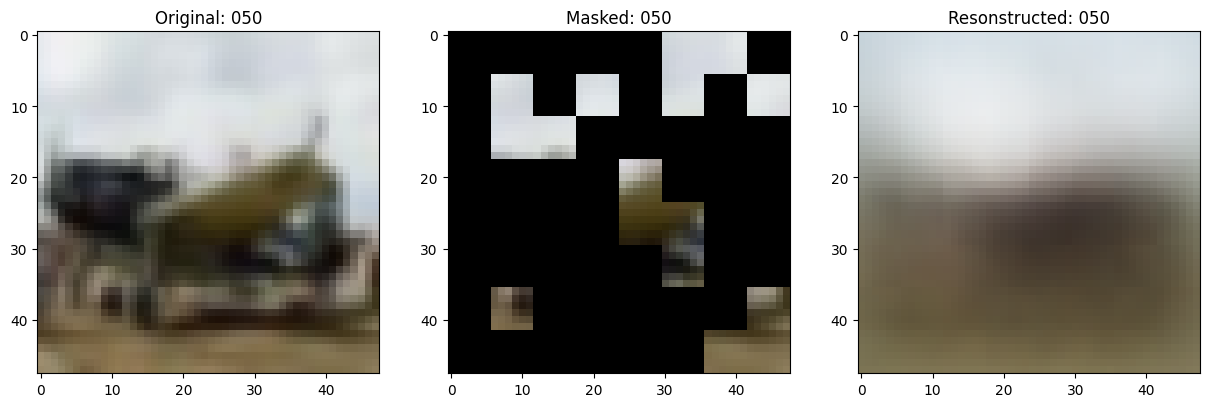
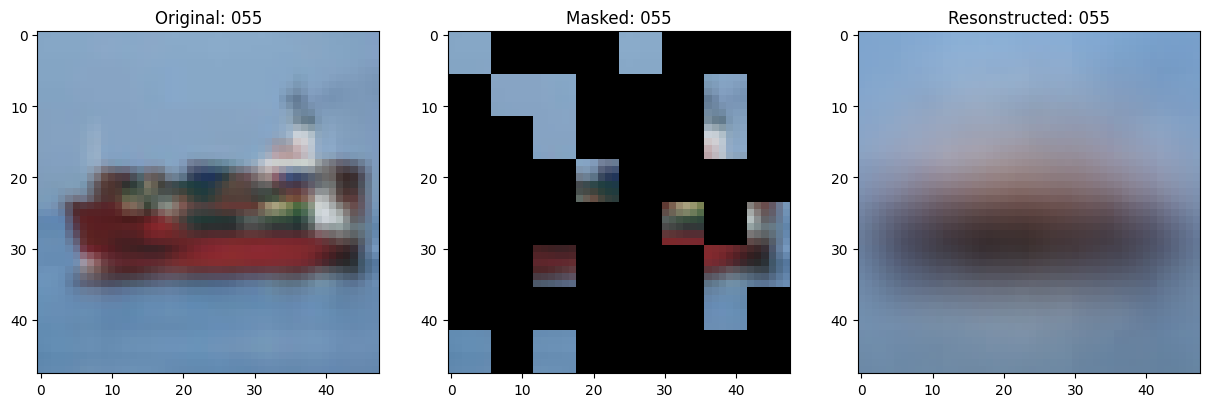
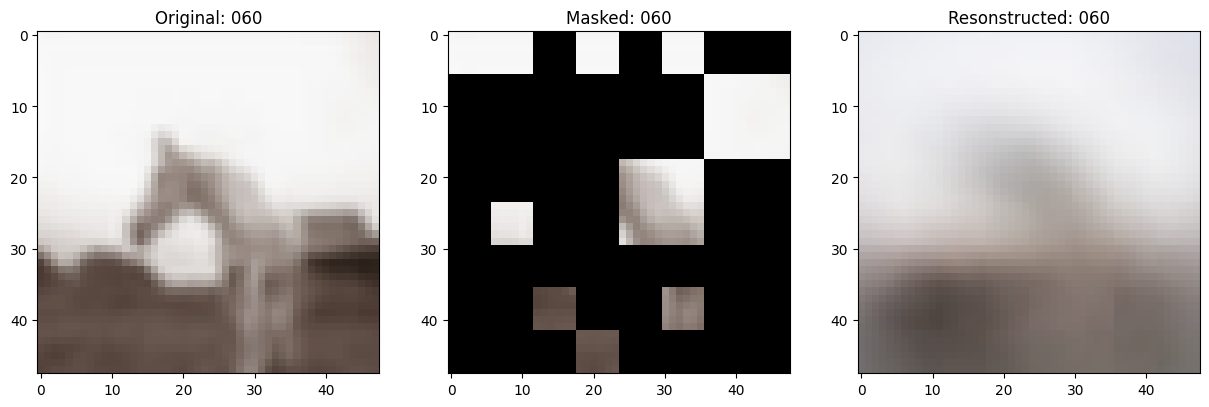
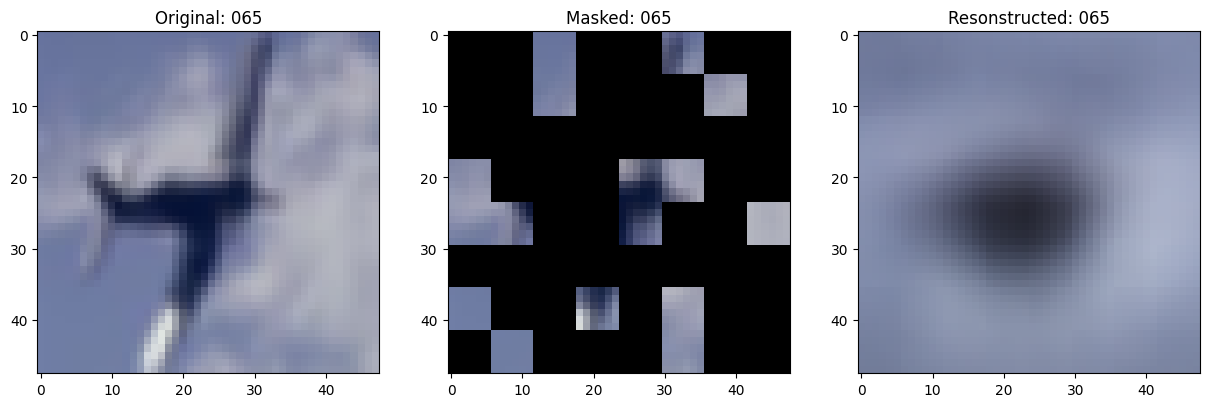
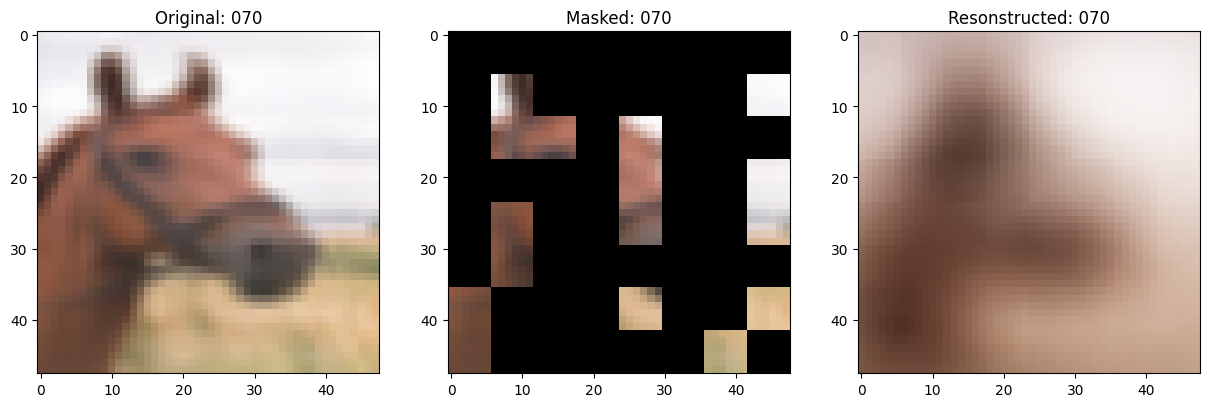
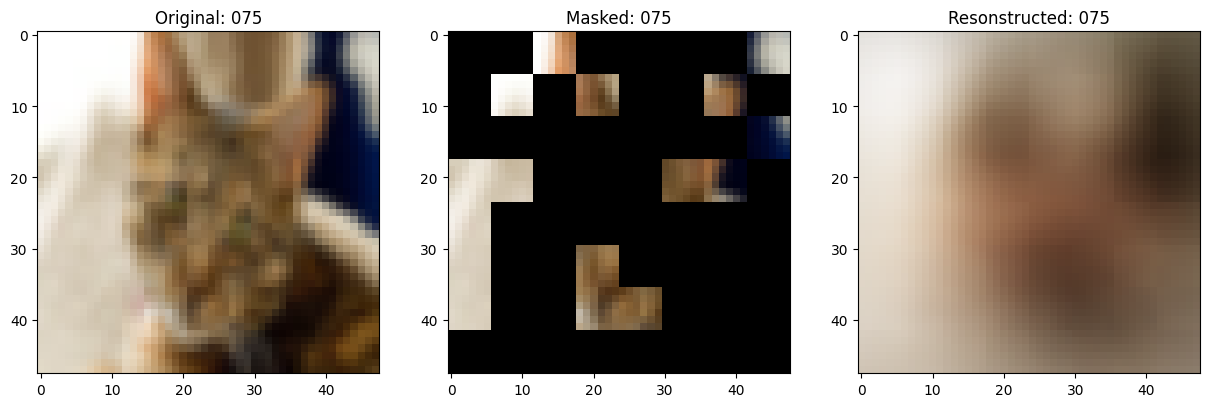
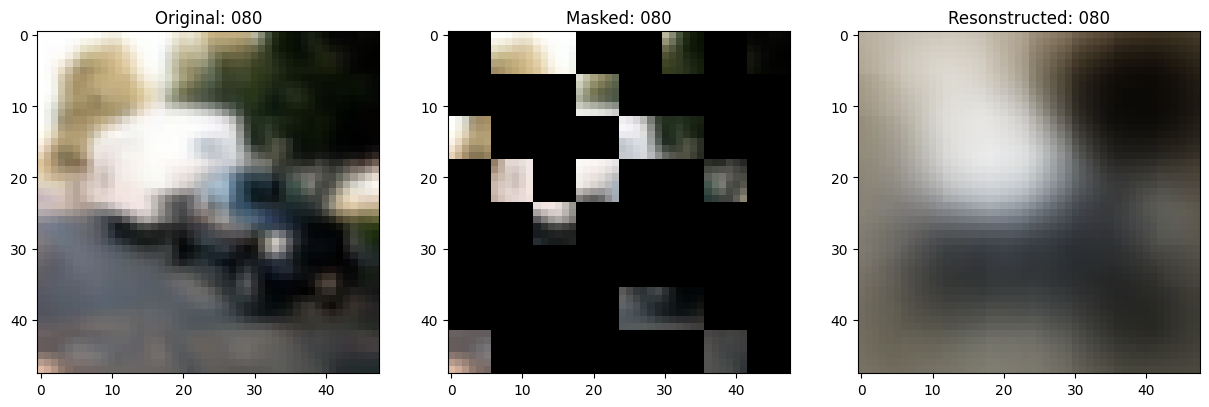
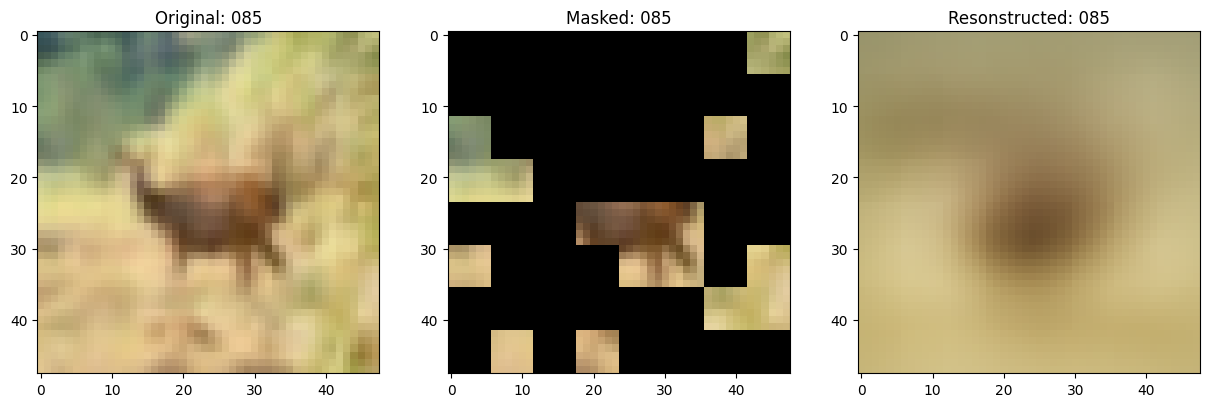
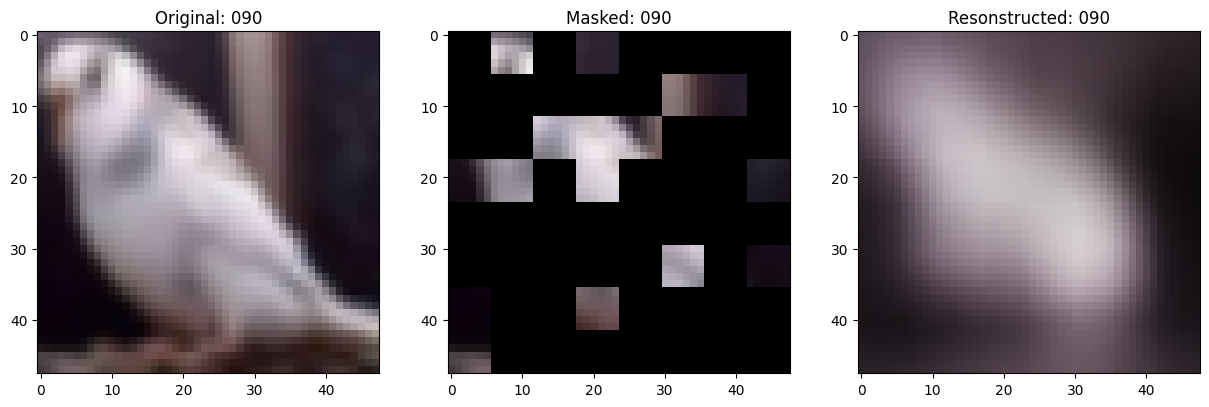
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
ax[0].imshow(original_image)
ax[0].set_title(f"Original: {epoch:03d}")
ax[1].imshow(masked_image)
ax[1].set_title(f"Masked: {epoch:03d}")
ax[2].imshow(reconstructed_image)
ax[2].set_title(f"Resonstructed: {epoch:03d}")
plt.show()
plt.close()
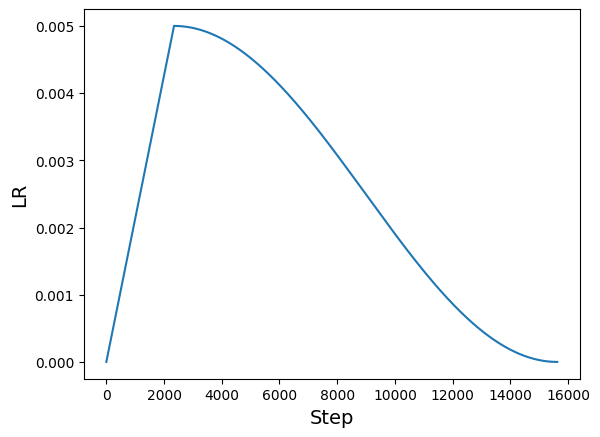
Learning rate scheduler
# Some code is taken from:
# https://www.kaggle.com/ashusma/training-rfcx-tensorflow-tpu-effnet-b2.
class WarmUpCosine(keras.optimizers.schedules.LearningRateSchedule):
def __init__(
self, learning_rate_base, total_steps, warmup_learning_rate, warmup_steps
):
super().__init__()
self.learning_rate_base = learning_rate_base
self.total_steps = total_steps
self.warmup_learning_rate = warmup_learning_rate
self.warmup_steps = warmup_steps
self.pi = tf.constant(np.pi)
def __call__(self, step):
if self.total_steps < self.warmup_steps:
raise ValueError("Total_steps must be larger or equal to warmup_steps.")
cos_annealed_lr = tf.cos(
self.pi
* (tf.cast(step, tf.float32) - self.warmup_steps)
/ float(self.total_steps - self.warmup_steps)
)
learning_rate = 0.5 * self.learning_rate_base * (1 + cos_annealed_lr)
if self.warmup_steps > 0:
if self.learning_rate_base < self.warmup_learning_rate:
raise ValueError(
"Learning_rate_base must be larger or equal to "
"warmup_learning_rate."
)
slope = (
self.learning_rate_base - self.warmup_learning_rate
) / self.warmup_steps
warmup_rate = slope * tf.cast(step, tf.float32) + self.warmup_learning_rate
learning_rate = tf.where(
step < self.warmup_steps, warmup_rate, learning_rate
)
return tf.where(
step > self.total_steps, 0.0, learning_rate, name="learning_rate"
)
total_steps = int((len(x_train) / BATCH_SIZE) * EPOCHS)
warmup_epoch_percentage = 0.15
warmup_steps = int(total_steps * warmup_epoch_percentage)
scheduled_lrs = WarmUpCosine(
learning_rate_base=LEARNING_RATE,
total_steps=total_steps,
warmup_learning_rate=0.0,
warmup_steps=warmup_steps,
)
lrs = [scheduled_lrs(step) for step in range(total_steps)]
plt.plot(lrs)
plt.xlabel("Step", fontsize=14)
plt.ylabel("LR", fontsize=14)
plt.show()
# Assemble the callbacks.
train_callbacks = [TrainMonitor(epoch_interval=5)]
Model compilation and training
optimizer = keras.optimizers.AdamW(
learning_rate=scheduled_lrs, weight_decay=WEIGHT_DECAY
)
# Compile and pretrain the model.
mae_model.compile(
optimizer=optimizer, loss=keras.losses.MeanSquaredError(), metrics=["mae"]
)
history = mae_model.fit(
train_ds,
epochs=EPOCHS,
validation_data=val_ds,
callbacks=train_callbacks,
)
# Measure its performance.
loss, mae = mae_model.evaluate(test_ds)
print(f"Loss: {loss:.2f}")
print(f"MAE: {mae:.2f}")
Epoch 1/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step - mae: 0.2035 - loss: 0.4828
Idx chosen: 92
157/157 ━━━━━━━━━━━━━━━━━━━━ 47s 95ms/step - mae: 0.2033 - loss: 0.4828 - val_loss: 0.5225 - val_mae: 0.1600
Epoch 2/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1592 - loss: 0.5128 - val_loss: 0.5290 - val_mae: 0.1511
Epoch 3/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1530 - loss: 0.5193 - val_loss: 0.5336 - val_mae: 0.1478
Epoch 4/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1502 - loss: 0.5220 - val_loss: 0.5298 - val_mae: 0.1436
Epoch 5/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1458 - loss: 0.5245 - val_loss: 0.5296 - val_mae: 0.1405
Epoch 6/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step - mae: 0.1414 - loss: 0.5265
Idx chosen: 14
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 88ms/step - mae: 0.1414 - loss: 0.5265 - val_loss: 0.5328 - val_mae: 0.1402
Epoch 7/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1399 - loss: 0.5278 - val_loss: 0.5361 - val_mae: 0.1360
Epoch 8/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1389 - loss: 0.5285 - val_loss: 0.5365 - val_mae: 0.1424
Epoch 9/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1379 - loss: 0.5295 - val_loss: 0.5312 - val_mae: 0.1345
Epoch 10/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1352 - loss: 0.5308 - val_loss: 0.5374 - val_mae: 0.1321
Epoch 11/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step - mae: 0.1339 - loss: 0.5317
Idx chosen: 106
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 87ms/step - mae: 0.1339 - loss: 0.5317 - val_loss: 0.5392 - val_mae: 0.1330
Epoch 12/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1321 - loss: 0.5331 - val_loss: 0.5383 - val_mae: 0.1301
Epoch 13/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1317 - loss: 0.5343 - val_loss: 0.5405 - val_mae: 0.1322
Epoch 14/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1326 - loss: 0.5338 - val_loss: 0.5404 - val_mae: 0.1280
Epoch 15/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.1297 - loss: 0.5343 - val_loss: 0.5444 - val_mae: 0.1261
Epoch 16/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 82ms/step - mae: 0.1276 - loss: 0.5361
Idx chosen: 71
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 91ms/step - mae: 0.1276 - loss: 0.5362 - val_loss: 0.5456 - val_mae: 0.1243
Epoch 17/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1262 - loss: 0.5382 - val_loss: 0.5427 - val_mae: 0.1233
Epoch 18/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1221 - loss: 0.5407 - val_loss: 0.5473 - val_mae: 0.1196
Epoch 19/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1209 - loss: 0.5412 - val_loss: 0.5511 - val_mae: 0.1176
Epoch 20/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1202 - loss: 0.5422 - val_loss: 0.5515 - val_mae: 0.1167
Epoch 21/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1186 - loss: 0.5430
Idx chosen: 188
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1186 - loss: 0.5430 - val_loss: 0.5546 - val_mae: 0.1168
Epoch 22/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1171 - loss: 0.5446 - val_loss: 0.5500 - val_mae: 0.1155
Epoch 23/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1161 - loss: 0.5457 - val_loss: 0.5559 - val_mae: 0.1135
Epoch 24/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1135 - loss: 0.5479 - val_loss: 0.5521 - val_mae: 0.1112
Epoch 25/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1128 - loss: 0.5480 - val_loss: 0.5505 - val_mae: 0.1122
Epoch 26/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1123 - loss: 0.5470
Idx chosen: 20
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1123 - loss: 0.5470 - val_loss: 0.5572 - val_mae: 0.1127
Epoch 27/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1114 - loss: 0.5487 - val_loss: 0.5555 - val_mae: 0.1092
Epoch 28/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1108 - loss: 0.5492 - val_loss: 0.5569 - val_mae: 0.1110
Epoch 29/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1104 - loss: 0.5491 - val_loss: 0.5517 - val_mae: 0.1110
Epoch 30/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1099 - loss: 0.5490 - val_loss: 0.5543 - val_mae: 0.1104
Epoch 31/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1095 - loss: 0.5501
Idx chosen: 102
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1095 - loss: 0.5501 - val_loss: 0.5578 - val_mae: 0.1108
Epoch 32/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1089 - loss: 0.5503 - val_loss: 0.5620 - val_mae: 0.1081
Epoch 33/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1079 - loss: 0.5509 - val_loss: 0.5618 - val_mae: 0.1067
Epoch 34/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1067 - loss: 0.5524 - val_loss: 0.5627 - val_mae: 0.1059
Epoch 35/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1068 - loss: 0.5515 - val_loss: 0.5576 - val_mae: 0.1050
Epoch 36/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1057 - loss: 0.5526
Idx chosen: 121
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1057 - loss: 0.5526 - val_loss: 0.5627 - val_mae: 0.1050
Epoch 37/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1065 - loss: 0.5534 - val_loss: 0.5638 - val_mae: 0.1050
Epoch 38/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1055 - loss: 0.5528 - val_loss: 0.5527 - val_mae: 0.1083
Epoch 39/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 20s 82ms/step - mae: 0.1056 - loss: 0.5516 - val_loss: 0.5562 - val_mae: 0.1044
Epoch 40/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1053 - loss: 0.5528 - val_loss: 0.5567 - val_mae: 0.1051
Epoch 41/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1049 - loss: 0.5533
Idx chosen: 210
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1049 - loss: 0.5533 - val_loss: 0.5620 - val_mae: 0.1030
Epoch 42/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1041 - loss: 0.5534 - val_loss: 0.5650 - val_mae: 0.1052
Epoch 43/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1048 - loss: 0.5526 - val_loss: 0.5619 - val_mae: 0.1027
Epoch 44/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1037 - loss: 0.5543 - val_loss: 0.5615 - val_mae: 0.1031
Epoch 45/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1036 - loss: 0.5535 - val_loss: 0.5575 - val_mae: 0.1026
Epoch 46/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1032 - loss: 0.5537
Idx chosen: 214
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1032 - loss: 0.5537 - val_loss: 0.5549 - val_mae: 0.1037
Epoch 47/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.1035 - loss: 0.5539 - val_loss: 0.5597 - val_mae: 0.1031
Epoch 48/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1033 - loss: 0.5533 - val_loss: 0.5650 - val_mae: 0.1013
Epoch 49/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.1027 - loss: 0.5543 - val_loss: 0.5571 - val_mae: 0.1028
Epoch 50/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1024 - loss: 0.5548 - val_loss: 0.5592 - val_mae: 0.1018
Epoch 51/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step - mae: 0.1025 - loss: 0.5543
Idx chosen: 74
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 85ms/step - mae: 0.1025 - loss: 0.5543 - val_loss: 0.5645 - val_mae: 0.1007
Epoch 52/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.1025 - loss: 0.5544 - val_loss: 0.5616 - val_mae: 0.1004
Epoch 53/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1014 - loss: 0.5547 - val_loss: 0.5594 - val_mae: 0.1007
Epoch 54/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1014 - loss: 0.5550 - val_loss: 0.5687 - val_mae: 0.1012
Epoch 55/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1022 - loss: 0.5551 - val_loss: 0.5572 - val_mae: 0.1018
Epoch 56/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1015 - loss: 0.5558
Idx chosen: 202
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1015 - loss: 0.5558 - val_loss: 0.5619 - val_mae: 0.0996
Epoch 57/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1008 - loss: 0.5550 - val_loss: 0.5614 - val_mae: 0.0996
Epoch 58/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1004 - loss: 0.5557 - val_loss: 0.5620 - val_mae: 0.0995
Epoch 59/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.1002 - loss: 0.5558 - val_loss: 0.5612 - val_mae: 0.0997
Epoch 60/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.1005 - loss: 0.5563 - val_loss: 0.5598 - val_mae: 0.1000
Epoch 61/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.1001 - loss: 0.5564
Idx chosen: 87
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.1001 - loss: 0.5564 - val_loss: 0.5606 - val_mae: 0.0998
Epoch 62/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.0998 - loss: 0.5562 - val_loss: 0.5643 - val_mae: 0.0988
Epoch 63/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.1001 - loss: 0.5556 - val_loss: 0.5657 - val_mae: 0.0985
Epoch 64/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0998 - loss: 0.5566 - val_loss: 0.5624 - val_mae: 0.0989
Epoch 65/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0994 - loss: 0.5564 - val_loss: 0.5576 - val_mae: 0.0999
Epoch 66/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 79ms/step - mae: 0.0993 - loss: 0.5567
Idx chosen: 116
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 86ms/step - mae: 0.0993 - loss: 0.5567 - val_loss: 0.5572 - val_mae: 0.1000
Epoch 67/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0990 - loss: 0.5570 - val_loss: 0.5619 - val_mae: 0.0981
Epoch 68/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0987 - loss: 0.5578 - val_loss: 0.5644 - val_mae: 0.0973
Epoch 69/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0981 - loss: 0.5577 - val_loss: 0.5639 - val_mae: 0.0976
Epoch 70/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0986 - loss: 0.5563 - val_loss: 0.5601 - val_mae: 0.0989
Epoch 71/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0982 - loss: 0.5578
Idx chosen: 99
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.0982 - loss: 0.5577 - val_loss: 0.5628 - val_mae: 0.0970
Epoch 72/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0979 - loss: 0.5569 - val_loss: 0.5637 - val_mae: 0.0968
Epoch 73/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0979 - loss: 0.5575 - val_loss: 0.5606 - val_mae: 0.0975
Epoch 74/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0977 - loss: 0.5572 - val_loss: 0.5628 - val_mae: 0.0967
Epoch 75/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0975 - loss: 0.5572 - val_loss: 0.5631 - val_mae: 0.0964
Epoch 76/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0973 - loss: 0.5580
Idx chosen: 103
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0973 - loss: 0.5579 - val_loss: 0.5628 - val_mae: 0.0967
Epoch 77/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0974 - loss: 0.5579 - val_loss: 0.5638 - val_mae: 0.0963
Epoch 78/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0968 - loss: 0.5585 - val_loss: 0.5615 - val_mae: 0.0967
Epoch 79/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0969 - loss: 0.5578 - val_loss: 0.5641 - val_mae: 0.0959
Epoch 80/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0967 - loss: 0.5584 - val_loss: 0.5619 - val_mae: 0.0962
Epoch 81/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0965 - loss: 0.5578
Idx chosen: 151
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0965 - loss: 0.5578 - val_loss: 0.5651 - val_mae: 0.0957
Epoch 82/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0965 - loss: 0.5583 - val_loss: 0.5644 - val_mae: 0.0957
Epoch 83/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0962 - loss: 0.5584 - val_loss: 0.5649 - val_mae: 0.0954
Epoch 84/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0962 - loss: 0.5586 - val_loss: 0.5611 - val_mae: 0.0962
Epoch 85/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0961 - loss: 0.5582 - val_loss: 0.5638 - val_mae: 0.0956
Epoch 86/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0961 - loss: 0.5584
Idx chosen: 130
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 83ms/step - mae: 0.0961 - loss: 0.5584 - val_loss: 0.5641 - val_mae: 0.0954
Epoch 87/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0959 - loss: 0.5580 - val_loss: 0.5641 - val_mae: 0.0953
Epoch 88/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0960 - loss: 0.5583 - val_loss: 0.5642 - val_mae: 0.0953
Epoch 89/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0958 - loss: 0.5591 - val_loss: 0.5635 - val_mae: 0.0953
Epoch 90/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0957 - loss: 0.5587 - val_loss: 0.5648 - val_mae: 0.0948
Epoch 91/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0957 - loss: 0.5585
Idx chosen: 149
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 84ms/step - mae: 0.0957 - loss: 0.5585 - val_loss: 0.5636 - val_mae: 0.0952
Epoch 92/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0957 - loss: 0.5593 - val_loss: 0.5642 - val_mae: 0.0950
Epoch 93/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0957 - loss: 0.5598 - val_loss: 0.5635 - val_mae: 0.0950
Epoch 94/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0956 - loss: 0.5587 - val_loss: 0.5641 - val_mae: 0.0950
Epoch 95/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0955 - loss: 0.5587 - val_loss: 0.5637 - val_mae: 0.0950
Epoch 96/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 0s 77ms/step - mae: 0.0956 - loss: 0.5585
Idx chosen: 52
157/157 ━━━━━━━━━━━━━━━━━━━━ 14s 87ms/step - mae: 0.0956 - loss: 0.5585 - val_loss: 0.5643 - val_mae: 0.0950
Epoch 97/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 81ms/step - mae: 0.0956 - loss: 0.5587 - val_loss: 0.5642 - val_mae: 0.0950
Epoch 98/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 82ms/step - mae: 0.0954 - loss: 0.5586 - val_loss: 0.5639 - val_mae: 0.0950
Epoch 99/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0954 - loss: 0.5580 - val_loss: 0.5641 - val_mae: 0.0950
Epoch 100/100
157/157 ━━━━━━━━━━━━━━━━━━━━ 13s 80ms/step - mae: 0.0955 - loss: 0.5587 - val_loss: 0.5639 - val_mae: 0.0951
40/40 ━━━━━━━━━━━━━━━━━━━━ 1s 13ms/step - mae: 0.0955 - loss: 0.5684
Loss: 0.57
MAE: 0.10
Evaluation with linear probing
Extract the encoder model along with other layers
# Extract the augmentation layers.
train_augmentation_model = mae_model.train_augmentation_model
test_augmentation_model = mae_model.test_augmentation_model
# Extract the patchers.
patch_layer = mae_model.patch_layer
patch_encoder = mae_model.patch_encoder
patch_encoder.downstream = True # Swtich the downstream flag to True.
# Extract the encoder.
encoder = mae_model.encoder
# Pack as a model.
downstream_model = keras.Sequential(
[
layers.Input((IMAGE_SIZE, IMAGE_SIZE, 3)),
patch_layer,
patch_encoder,
encoder,
layers.BatchNormalization(), # Refer to A.1 (Linear probing).
layers.GlobalAveragePooling1D(),
layers.Dense(NUM_CLASSES, activation="softmax"),
],
name="linear_probe_model",
)
# Only the final classification layer of the `downstream_model` should be trainable.
for layer in downstream_model.layers[:-1]:
layer.trainable = False
downstream_model.summary()
Model: "linear_probe_model"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩ │ patches_1 (Patches) │ (None, 64, 108) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ patch_encoder_1 (PatchEncoder) │ (None, 64, 128) │ 22,144 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ mae_encoder (Functional) │ (None, 64, 128) │ 1,981,696 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ batch_normalization │ (None, 64, 128) │ 512 │ │ (BatchNormalization) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ global_average_pooling1d │ (None, 128) │ 0 │ │ (GlobalAveragePooling1D) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dense_20 (Dense) │ (None, 10) │ 1,290 │ └─────────────────────────────────┴───────────────────────────┴────────────┘
Total params: 2,005,642 (7.65 MB)
Trainable params: 1,290 (5.04 KB)
Non-trainable params: 2,004,352 (7.65 MB)
We are using average pooling to extract learned representations from the MAE encoder. Another approach would be to use a learnable dummy token inside the encoder during pretraining (resembling the [CLS] token). Then we can extract representations from that token during the downstream tasks.
Prepare datasets for linear probing
def prepare_data(images, labels, is_train=True):
if is_train:
augmentation_model = train_augmentation_model
else:
augmentation_model = test_augmentation_model
dataset = tf.data.Dataset.from_tensor_slices((images, labels))
if is_train:
dataset = dataset.shuffle(BUFFER_SIZE)
dataset = dataset.batch(BATCH_SIZE).map(
lambda x, y: (augmentation_model(x), y), num_parallel_calls=AUTO
)
return dataset.prefetch(AUTO)
train_ds = prepare_data(x_train, y_train)
val_ds = prepare_data(x_train, y_train, is_train=False)
test_ds = prepare_data(x_test, y_test, is_train=False)
Perform linear probing
linear_probe_epochs = 50
linear_prob_lr = 0.1
warm_epoch_percentage = 0.1
steps = int((len(x_train) // BATCH_SIZE) * linear_probe_epochs)
warmup_steps = int(steps * warm_epoch_percentage)
scheduled_lrs = WarmUpCosine(
learning_rate_base=linear_prob_lr,
total_steps=steps,
warmup_learning_rate=0.0,
warmup_steps=warmup_steps,
)
optimizer = keras.optimizers.SGD(learning_rate=scheduled_lrs, momentum=0.9)
downstream_model.compile(
optimizer=optimizer, loss="sparse_categorical_crossentropy", metrics=["accuracy"]
)
downstream_model.fit(train_ds, validation_data=val_ds, epochs=linear_probe_epochs)
loss, accuracy = downstream_model.evaluate(test_ds)
accuracy = round(accuracy * 100, 2)
print(f"Accuracy on the test set: {accuracy}%.")
Epoch 1/50
7/157 [37m━━━━━━━━━━━━━━━━━━━━ 3s 21ms/step - accuracy: 0.1183 - loss: 3.3939
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1700264823.481598 64012 device_compiler.h:187] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
157/157 ━━━━━━━━━━━━━━━━━━━━ 70s 242ms/step - accuracy: 0.1967 - loss: 2.6073 - val_accuracy: 0.3631 - val_loss: 1.7846
Epoch 2/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.3521 - loss: 1.8063 - val_accuracy: 0.3677 - val_loss: 1.7301
Epoch 3/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3580 - loss: 1.7580 - val_accuracy: 0.3649 - val_loss: 1.7326
Epoch 4/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3617 - loss: 1.7471 - val_accuracy: 0.3810 - val_loss: 1.7353
Epoch 5/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - accuracy: 0.3547 - loss: 1.7728 - val_accuracy: 0.3526 - val_loss: 1.8496
Epoch 6/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - accuracy: 0.3546 - loss: 1.7866 - val_accuracy: 0.3896 - val_loss: 1.7583
Epoch 7/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - accuracy: 0.3587 - loss: 1.7924 - val_accuracy: 0.3674 - val_loss: 1.7729
Epoch 8/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 38ms/step - accuracy: 0.3616 - loss: 1.7912 - val_accuracy: 0.3685 - val_loss: 1.7928
Epoch 9/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 36ms/step - accuracy: 0.3707 - loss: 1.7543 - val_accuracy: 0.3568 - val_loss: 1.7943
Epoch 10/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3719 - loss: 1.7451 - val_accuracy: 0.3859 - val_loss: 1.7230
Epoch 11/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3781 - loss: 1.7384 - val_accuracy: 0.3711 - val_loss: 1.7608
Epoch 12/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - accuracy: 0.3791 - loss: 1.7249 - val_accuracy: 0.4004 - val_loss: 1.6961
Epoch 13/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3818 - loss: 1.7303 - val_accuracy: 0.3501 - val_loss: 1.8506
Epoch 14/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3841 - loss: 1.7179 - val_accuracy: 0.3810 - val_loss: 1.8033
Epoch 15/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3818 - loss: 1.7172 - val_accuracy: 0.4168 - val_loss: 1.6507
Epoch 16/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 36ms/step - accuracy: 0.3851 - loss: 1.7059 - val_accuracy: 0.3806 - val_loss: 1.7581
Epoch 17/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3747 - loss: 1.7356 - val_accuracy: 0.4094 - val_loss: 1.6466
Epoch 18/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.3828 - loss: 1.7221 - val_accuracy: 0.4015 - val_loss: 1.6757
Epoch 19/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3889 - loss: 1.6939 - val_accuracy: 0.4102 - val_loss: 1.6392
Epoch 20/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3943 - loss: 1.6857 - val_accuracy: 0.4028 - val_loss: 1.6518
Epoch 21/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3870 - loss: 1.6970 - val_accuracy: 0.3949 - val_loss: 1.7283
Epoch 22/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3893 - loss: 1.6838 - val_accuracy: 0.4207 - val_loss: 1.6292
Epoch 23/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.4005 - loss: 1.6606 - val_accuracy: 0.4152 - val_loss: 1.6320
Epoch 24/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3978 - loss: 1.6556 - val_accuracy: 0.4042 - val_loss: 1.6657
Epoch 25/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4029 - loss: 1.6464 - val_accuracy: 0.4198 - val_loss: 1.6033
Epoch 26/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.3974 - loss: 1.6638 - val_accuracy: 0.4278 - val_loss: 1.5731
Epoch 27/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - accuracy: 0.4035 - loss: 1.6370 - val_accuracy: 0.4302 - val_loss: 1.5663
Epoch 28/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4027 - loss: 1.6349 - val_accuracy: 0.4458 - val_loss: 1.5349
Epoch 29/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4054 - loss: 1.6196 - val_accuracy: 0.4349 - val_loss: 1.5709
Epoch 30/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.4070 - loss: 1.6061 - val_accuracy: 0.4297 - val_loss: 1.5578
Epoch 31/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4105 - loss: 1.6172 - val_accuracy: 0.4250 - val_loss: 1.5735
Epoch 32/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4197 - loss: 1.5960 - val_accuracy: 0.4259 - val_loss: 1.5677
Epoch 33/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4156 - loss: 1.5989 - val_accuracy: 0.4400 - val_loss: 1.5395
Epoch 34/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.4214 - loss: 1.5862 - val_accuracy: 0.4486 - val_loss: 1.5237
Epoch 35/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4208 - loss: 1.5763 - val_accuracy: 0.4188 - val_loss: 1.5925
Epoch 36/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4227 - loss: 1.5803 - val_accuracy: 0.4525 - val_loss: 1.5174
Epoch 37/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4267 - loss: 1.5700 - val_accuracy: 0.4463 - val_loss: 1.5330
Epoch 38/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 37ms/step - accuracy: 0.4283 - loss: 1.5649 - val_accuracy: 0.4348 - val_loss: 1.5482
Epoch 39/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4332 - loss: 1.5581 - val_accuracy: 0.4486 - val_loss: 1.5251
Epoch 40/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4290 - loss: 1.5596 - val_accuracy: 0.4489 - val_loss: 1.5221
Epoch 41/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4318 - loss: 1.5589 - val_accuracy: 0.4494 - val_loss: 1.5202
Epoch 42/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4317 - loss: 1.5514 - val_accuracy: 0.4505 - val_loss: 1.5184
Epoch 43/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4353 - loss: 1.5504 - val_accuracy: 0.4561 - val_loss: 1.5081
Epoch 44/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4369 - loss: 1.5510 - val_accuracy: 0.4581 - val_loss: 1.5092
Epoch 45/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 35ms/step - accuracy: 0.4379 - loss: 1.5428 - val_accuracy: 0.4555 - val_loss: 1.5099
Epoch 46/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4421 - loss: 1.5475 - val_accuracy: 0.4579 - val_loss: 1.5073
Epoch 47/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4434 - loss: 1.5390 - val_accuracy: 0.4593 - val_loss: 1.5052
Epoch 48/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 34ms/step - accuracy: 0.4418 - loss: 1.5373 - val_accuracy: 0.4600 - val_loss: 1.5038
Epoch 49/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 6s 38ms/step - accuracy: 0.4400 - loss: 1.5367 - val_accuracy: 0.4596 - val_loss: 1.5045
Epoch 50/50
157/157 ━━━━━━━━━━━━━━━━━━━━ 5s 35ms/step - accuracy: 0.4448 - loss: 1.5321 - val_accuracy: 0.4595 - val_loss: 1.5048
40/40 ━━━━━━━━━━━━━━━━━━━━ 3s 71ms/step - accuracy: 0.4496 - loss: 1.5088
Accuracy on the test set: 44.66%.
We believe that with a more sophisticated hyperparameter tuning process and a longer pretraining it is possible to improve this performance further. For comparison, we took the encoder architecture and trained it from scratch in a fully supervised manner. This gave us ~76% test top-1 accuracy. The authors of MAE demonstrates strong performance on the ImageNet-1k dataset as well as other downstream tasks like object detection and semantic segmentation.
Final notes
We refer the interested readers to other examples on self-supervised learning present on keras.io:
This idea of using BERT flavored pretraining in computer vision was also explored in Selfie, but it could not demonstrate strong results. Another concurrent work that explores the idea of masked image modeling is SimMIM. Finally, as a fun fact, we, the authors of this example also explored the idea of "reconstruction as a pretext task" in 2020 but we could not prevent the network from representation collapse, and hence we did not get strong downstream performance.
We would like to thank Xinlei Chen (one of the authors of MAE) for helpful discussions. We are grateful to JarvisLabs and Google Developers Experts program for helping with GPU credits.