A walk through latent space with Stable Diffusion 3
Authors: Hongyu Chiu, Ian Stenbit, fchollet, lukewood
Date created: 2024/11/11
Last modified: 2024/11/11
Description: Explore the latent manifold of Stable Diffusion 3.
Overview
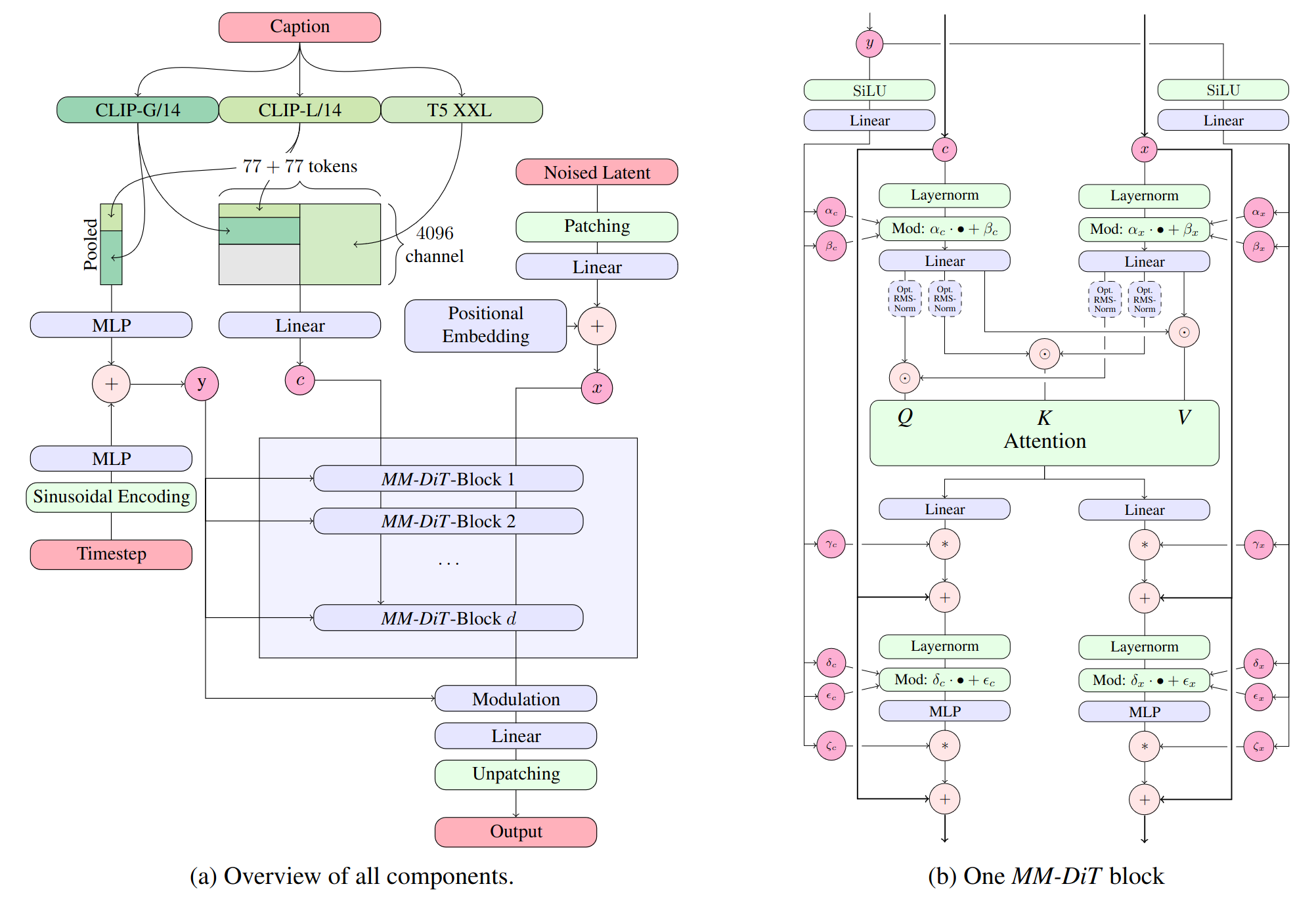
Generative image models learn a "latent manifold" of the visual world: a low-dimensional vector space where each point maps to an image. Going from such a point on the manifold back to a displayable image is called "decoding" – in the Stable Diffusion model, this is handled by the "decoder" model.
This latent manifold of images is continuous and interpolative, meaning that:
- Moving a little on the manifold only changes the corresponding image a little (continuity).
- For any two points A and B on the manifold (i.e. any two images), it is possible to move from A to B via a path where each intermediate point is also on the manifold (i.e. is also a valid image). Intermediate points would be called "interpolations" between the two starting images.
Stable Diffusion isn't just an image model, though, it's also a natural language model. It has two latent spaces: the image representation space learned by the encoder used during training, and the prompt latent space which is learned using a combination of pretraining and training-time fine-tuning.
Latent space walking, or latent space exploration, is the process of sampling a point in latent space and incrementally changing the latent representation. Its most common application is generating animations where each sampled point is fed to the decoder and is stored as a frame in the final animation. For high-quality latent representations, this produces coherent-looking animations. These animations can provide insight into the feature map of the latent space, and can ultimately lead to improvements in the training process. One such GIF is displayed below:

In this guide, we will show how to take advantage of the TextToImage API in KerasHub to perform prompt interpolation and circular walks through Stable Diffusion 3's visual latent manifold, as well as through the text encoder's latent manifold.
This guide assumes the reader has a high-level understanding of Stable Diffusion 3. If you haven't already, you should start by reading the Stable Diffusion 3 in KerasHub.
It is also worth noting that the preset "stable_diffusion_3_medium" excludes the T5XXL text encoder, as it requires significantly more GPU memory. The performace degradation is negligible in most cases. The weights, including T5XXL, will be available on KerasHub soon.
!# Use the latest version of KerasHub
!!pip install -Uq git+https://github.com/keras-team/keras-hub.git
import math
import keras
import keras_hub
import matplotlib.pyplot as plt
from keras import ops
from keras import random
from PIL import Image
height, width = 512, 512
num_steps = 28
guidance_scale = 7.0
dtype = "float16"
# Instantiate the Stable Diffusion 3 model and the preprocessor
backbone = keras_hub.models.StableDiffusion3Backbone.from_preset(
"stable_diffusion_3_medium", image_shape=(height, width, 3), dtype=dtype
)
preprocessor = keras_hub.models.StableDiffusion3TextToImagePreprocessor.from_preset(
"stable_diffusion_3_medium"
)
Let's define some helper functions for this example.
def get_text_embeddings(prompt):
"""Get the text embeddings for a given prompt."""
token_ids = preprocessor.generate_preprocess([prompt])
negative_token_ids = preprocessor.generate_preprocess([""])
(
positive_embeddings,
negative_embeddings,
positive_pooled_embeddings,
negative_pooled_embeddings,
) = backbone.encode_text_step(token_ids, negative_token_ids)
return (
positive_embeddings,
negative_embeddings,
positive_pooled_embeddings,
negative_pooled_embeddings,
)
def decode_to_images(x, height, width):
"""Concatenate and normalize the images to uint8 dtype."""
x = ops.concatenate(x, axis=0)
x = ops.reshape(x, (-1, height, width, 3))
x = ops.clip(ops.divide(ops.add(x, 1.0), 2.0), 0.0, 1.0)
return ops.cast(ops.round(ops.multiply(x, 255.0)), "uint8")
def generate_with_latents_and_embeddings(
latents, embeddings, num_steps, guidance_scale
):
"""Generate images from latents and text embeddings."""
def body_fun(step, latents):
return backbone.denoise_step(
latents,
embeddings,
step,
num_steps,
guidance_scale,
)
latents = ops.fori_loop(0, num_steps, body_fun, latents)
return backbone.decode_step(latents)
def export_as_gif(filename, images, frames_per_second=10, no_rubber_band=False):
if not no_rubber_band:
images += images[2:-1][::-1] # Makes a rubber band: A->B->A
images[0].save(
filename,
save_all=True,
append_images=images[1:],
duration=1000 // frames_per_second,
loop=0,
)
We are going to generate images using custom latents and embeddings, so we need
to implement the generate_with_latents_and_embeddings function. Additionally,
it is important to compile this function to speed up the generation process.
if keras.config.backend() == "torch":
import torch
@torch.no_grad()
def wrapped_function(*args, **kwargs):
return generate_with_latents_and_embeddings(*args, **kwargs)
generate_function = wrapped_function
elif keras.config.backend() == "tensorflow":
import tensorflow as tf
generate_function = tf.function(
generate_with_latents_and_embeddings, jit_compile=True
)
elif keras.config.backend() == "jax":
import itertools
import jax
@jax.jit
def compiled_function(state, *args, **kwargs):
(trainable_variables, non_trainable_variables) = state
mapping = itertools.chain(
zip(backbone.trainable_variables, trainable_variables),
zip(backbone.non_trainable_variables, non_trainable_variables),
)
with keras.StatelessScope(state_mapping=mapping):
return generate_with_latents_and_embeddings(*args, **kwargs)
def wrapped_function(*args, **kwargs):
state = (
[v.value for v in backbone.trainable_variables],
[v.value for v in backbone.non_trainable_variables],
)
return compiled_function(state, *args, **kwargs)
generate_function = wrapped_function
Interpolating between text prompts
In Stable Diffusion 3, a text prompt is encoded into multiple vectors, which are then used to guide the diffusion process. These latent encoding vectors have shapes of 154x4096 and 2048 for both the positive and negative prompts - quite large! When we input a text prompt into Stable Diffusion 3, we generate images from a single point on this latent manifold.
To explore more of this manifold, we can interpolate between two text encodings and generate images at those interpolated points:
prompt_1 = "A cute dog in a beautiful field of lavander colorful flowers "
prompt_1 += "everywhere, perfect lighting, leica summicron 35mm f2.0, kodak "
prompt_1 += "portra 400, film grain"
prompt_2 = prompt_1.replace("dog", "cat")
interpolation_steps = 5
encoding_1 = get_text_embeddings(prompt_1)
encoding_2 = get_text_embeddings(prompt_2)
# Show the size of the latent manifold
print(f"Positive embeddings shape: {encoding_1[0].shape}")
print(f"Negative embeddings shape: {encoding_1[1].shape}")
print(f"Positive pooled embeddings shape: {encoding_1[2].shape}")
print(f"Negative pooled embeddings shape: {encoding_1[3].shape}")
Positive embeddings shape: (1, 154, 4096)
Negative embeddings shape: (1, 154, 4096)
Positive pooled embeddings shape: (1, 2048)
Negative pooled embeddings shape: (1, 2048)
In this example, we want to use Spherical Linear Interpolation (slerp) instead of simple linear interpolation. Slerp is commonly used in computer graphics to animate rotations smoothly and can also be applied to interpolate between high-dimensional data points, such as latent vectors used in generative models.
The source is from Andrej Karpathy's gist: https://gist.github.com/karpathy/00103b0037c5aaea32fe1da1af553355.
A more detailed explanation of this method can be found at: https://en.wikipedia.org/wiki/Slerp.
def slerp(v1, v2, num):
ori_dtype = v1.dtype
# Cast to float32 for numerical stability.
v1 = ops.cast(v1, "float32")
v2 = ops.cast(v2, "float32")
def interpolation(t, v1, v2, dot_threshold=0.9995):
"""helper function to spherically interpolate two arrays."""
dot = ops.sum(
v1 * v2 / (ops.linalg.norm(ops.ravel(v1)) * ops.linalg.norm(ops.ravel(v2)))
)
if ops.abs(dot) > dot_threshold:
v2 = (1 - t) * v1 + t * v2
else:
theta_0 = ops.arccos(dot)
sin_theta_0 = ops.sin(theta_0)
theta_t = theta_0 * t
sin_theta_t = ops.sin(theta_t)
s0 = ops.sin(theta_0 - theta_t) / sin_theta_0
s1 = sin_theta_t / sin_theta_0
v2 = s0 * v1 + s1 * v2
return v2
t = ops.linspace(0, 1, num)
interpolated = ops.stack([interpolation(t[i], v1, v2) for i in range(num)], axis=0)
return ops.cast(interpolated, ori_dtype)
interpolated_positive_embeddings = slerp(
encoding_1[0], encoding_2[0], interpolation_steps
)
interpolated_positive_pooled_embeddings = slerp(
encoding_1[2], encoding_2[2], interpolation_steps
)
# We don't use negative prompts in this example, so there’s no need to
# interpolate them.
negative_embeddings = encoding_1[1]
negative_pooled_embeddings = encoding_1[3]
Once we've interpolated the encodings, we can generate images from each point. Note that in order to maintain some stability between the resulting images we keep the diffusion latents constant between images.
latents = random.normal((1, height // 8, width // 8, 16), seed=42)
images = []
progbar = keras.utils.Progbar(interpolation_steps)
for i in range(interpolation_steps):
images.append(
generate_function(
latents,
(
interpolated_positive_embeddings[i],
negative_embeddings,
interpolated_positive_pooled_embeddings[i],
negative_pooled_embeddings,
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == interpolation_steps - 1)
Now that we've generated some interpolated images, let's take a look at them!
Throughout this tutorial, we're going to export sequences of images as gifs so that they can be easily viewed with some temporal context. For sequences of images where the first and last images don't match conceptually, we rubber-band the gif.
If you're running in Colab, you can view your own GIFs by running:
from IPython.display import Image as IImage
IImage("dog_to_cat_5.gif")
images = ops.convert_to_numpy(decode_to_images(images, height, width))
export_as_gif(
"dog_to_cat_5.gif",
[Image.fromarray(image) for image in images],
frames_per_second=2,
)

The results may seem surprising. Generally, interpolating between prompts produces coherent looking images, and often demonstrates a progressive concept shift between the contents of the two prompts. This is indicative of a high quality representation space, that closely mirrors the natural structure of the visual world.
To best visualize this, we should do a much more fine-grained interpolation, using more steps.
interpolation_steps = 64
batch_size = 4
batches = interpolation_steps // batch_size
interpolated_positive_embeddings = slerp(
encoding_1[0], encoding_2[0], interpolation_steps
)
interpolated_positive_pooled_embeddings = slerp(
encoding_1[2], encoding_2[2], interpolation_steps
)
positive_embeddings_shape = ops.shape(encoding_1[0])
positive_pooled_embeddings_shape = ops.shape(encoding_1[2])
interpolated_positive_embeddings = ops.reshape(
interpolated_positive_embeddings,
(
batches,
batch_size,
positive_embeddings_shape[-2],
positive_embeddings_shape[-1],
),
)
interpolated_positive_pooled_embeddings = ops.reshape(
interpolated_positive_pooled_embeddings,
(batches, batch_size, positive_pooled_embeddings_shape[-1]),
)
negative_embeddings = ops.tile(encoding_1[1], (batch_size, 1, 1))
negative_pooled_embeddings = ops.tile(encoding_1[3], (batch_size, 1))
latents = random.normal((1, height // 8, width // 8, 16), seed=42)
latents = ops.tile(latents, (batch_size, 1, 1, 1))
images = []
progbar = keras.utils.Progbar(batches)
for i in range(batches):
images.append(
generate_function(
latents,
(
interpolated_positive_embeddings[i],
negative_embeddings,
interpolated_positive_pooled_embeddings[i],
negative_pooled_embeddings,
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == batches - 1)
images = ops.convert_to_numpy(decode_to_images(images, height, width))
export_as_gif(
"dog_to_cat_64.gif",
[Image.fromarray(image) for image in images],
frames_per_second=2,
)

The resulting gif shows a much clearer and more coherent shift between the two prompts. Try out some prompts of your own and experiment!
We can even extend this concept for more than one image. For example, we can interpolate between four prompts:
prompt_1 = "A watercolor painting of a Golden Retriever at the beach"
prompt_2 = "A still life DSLR photo of a bowl of fruit"
prompt_3 = "The eiffel tower in the style of starry night"
prompt_4 = "An architectural sketch of a skyscraper"
interpolation_steps = 8
batch_size = 4
batches = (interpolation_steps**2) // batch_size
encoding_1 = get_text_embeddings(prompt_1)
encoding_2 = get_text_embeddings(prompt_2)
encoding_3 = get_text_embeddings(prompt_3)
encoding_4 = get_text_embeddings(prompt_4)
positive_embeddings_shape = ops.shape(encoding_1[0])
positive_pooled_embeddings_shape = ops.shape(encoding_1[2])
interpolated_positive_embeddings_12 = slerp(
encoding_1[0], encoding_2[0], interpolation_steps
)
interpolated_positive_embeddings_34 = slerp(
encoding_3[0], encoding_4[0], interpolation_steps
)
interpolated_positive_embeddings = slerp(
interpolated_positive_embeddings_12,
interpolated_positive_embeddings_34,
interpolation_steps,
)
interpolated_positive_embeddings = ops.reshape(
interpolated_positive_embeddings,
(
batches,
batch_size,
positive_embeddings_shape[-2],
positive_embeddings_shape[-1],
),
)
interpolated_positive_pooled_embeddings_12 = slerp(
encoding_1[2], encoding_2[2], interpolation_steps
)
interpolated_positive_pooled_embeddings_34 = slerp(
encoding_3[2], encoding_4[2], interpolation_steps
)
interpolated_positive_pooled_embeddings = slerp(
interpolated_positive_pooled_embeddings_12,
interpolated_positive_pooled_embeddings_34,
interpolation_steps,
)
interpolated_positive_pooled_embeddings = ops.reshape(
interpolated_positive_pooled_embeddings,
(batches, batch_size, positive_pooled_embeddings_shape[-1]),
)
negative_embeddings = ops.tile(encoding_1[1], (batch_size, 1, 1))
negative_pooled_embeddings = ops.tile(encoding_1[3], (batch_size, 1))
latents = random.normal((1, height // 8, width // 8, 16), seed=42)
latents = ops.tile(latents, (batch_size, 1, 1, 1))
images = []
progbar = keras.utils.Progbar(batches)
for i in range(batches):
images.append(
generate_function(
latents,
(
interpolated_positive_embeddings[i],
negative_embeddings,
interpolated_positive_pooled_embeddings[i],
negative_pooled_embeddings,
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == batches - 1)
Let's display the resulting images in a grid to make them easier to interpret.
def plot_grid(images, path, grid_size, scale=2):
fig, axs = plt.subplots(
grid_size, grid_size, figsize=(grid_size * scale, grid_size * scale)
)
fig.tight_layout()
plt.subplots_adjust(wspace=0, hspace=0)
plt.axis("off")
for ax in axs.flat:
ax.axis("off")
for i in range(min(grid_size * grid_size, len(images))):
ax = axs.flat[i]
ax.imshow(images[i])
ax.axis("off")
for i in range(len(images), grid_size * grid_size):
axs.flat[i].axis("off")
axs.flat[i].remove()
plt.savefig(
fname=path,
pad_inches=0,
bbox_inches="tight",
transparent=False,
dpi=60,
)
images = ops.convert_to_numpy(decode_to_images(images, height, width))
plot_grid(images, "4-way-interpolation.jpg", interpolation_steps)

We can also interpolate while allowing diffusion latents to vary by dropping
the seed parameter:
images = []
progbar = keras.utils.Progbar(batches)
for i in range(batches):
# Vary diffusion latents for each input.
latents = random.normal((batch_size, height // 8, width // 8, 16))
images.append(
generate_function(
latents,
(
interpolated_positive_embeddings[i],
negative_embeddings,
interpolated_positive_pooled_embeddings[i],
negative_pooled_embeddings,
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == batches - 1)
images = ops.convert_to_numpy(decode_to_images(images, height, width))
plot_grid(images, "4-way-interpolation-varying-latent.jpg", interpolation_steps)

Next up – let's go for some walks!
A walk around a text prompt
Our next experiment will be to go for a walk around the latent manifold starting from a point produced by a particular prompt.
walk_steps = 64
batch_size = 4
batches = walk_steps // batch_size
step_size = 0.01
prompt = "The eiffel tower in the style of starry night"
encoding = get_text_embeddings(prompt)
positive_embeddings = encoding[0]
positive_pooled_embeddings = encoding[2]
negative_embeddings = encoding[1]
negative_pooled_embeddings = encoding[3]
# The shape of `positive_embeddings`: (1, 154, 4096)
# The shape of `positive_pooled_embeddings`: (1, 2048)
positive_embeddings_delta = ops.ones_like(positive_embeddings) * step_size
positive_pooled_embeddings_delta = ops.ones_like(positive_pooled_embeddings) * step_size
positive_embeddings_shape = ops.shape(positive_embeddings)
positive_pooled_embeddings_shape = ops.shape(positive_pooled_embeddings)
walked_positive_embeddings = []
walked_positive_pooled_embeddings = []
for step_index in range(walk_steps):
walked_positive_embeddings.append(positive_embeddings)
walked_positive_pooled_embeddings.append(positive_pooled_embeddings)
positive_embeddings += positive_embeddings_delta
positive_pooled_embeddings += positive_pooled_embeddings_delta
walked_positive_embeddings = ops.stack(walked_positive_embeddings, axis=0)
walked_positive_pooled_embeddings = ops.stack(walked_positive_pooled_embeddings, axis=0)
walked_positive_embeddings = ops.reshape(
walked_positive_embeddings,
(
batches,
batch_size,
positive_embeddings_shape[-2],
positive_embeddings_shape[-1],
),
)
walked_positive_pooled_embeddings = ops.reshape(
walked_positive_pooled_embeddings,
(batches, batch_size, positive_pooled_embeddings_shape[-1]),
)
negative_embeddings = ops.tile(encoding_1[1], (batch_size, 1, 1))
negative_pooled_embeddings = ops.tile(encoding_1[3], (batch_size, 1))
latents = random.normal((1, height // 8, width // 8, 16), seed=42)
latents = ops.tile(latents, (batch_size, 1, 1, 1))
images = []
progbar = keras.utils.Progbar(batches)
for i in range(batches):
images.append(
generate_function(
latents,
(
walked_positive_embeddings[i],
negative_embeddings,
walked_positive_pooled_embeddings[i],
negative_pooled_embeddings,
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == batches - 1)
images = ops.convert_to_numpy(decode_to_images(images, height, width))
export_as_gif(
"eiffel-tower-starry-night.gif",
[Image.fromarray(image) for image in images],
frames_per_second=2,
)

Perhaps unsurprisingly, walking too far from the encoder's latent manifold
produces images that look incoherent. Try it for yourself by setting your own
prompt, and adjusting step_size to increase or decrease the magnitude
of the walk. Note that when the magnitude of the walk gets large, the walk often
leads into areas which produce extremely noisy images.
A circular walk through the diffusion latent space for a single prompt
Our final experiment is to stick to one prompt and explore the variety of images that the diffusion model can produce from that prompt. We do this by controlling the noise that is used to seed the diffusion process.
We create two noise components, x and y, and do a walk from 0 to 2π, summing
the cosine of our x component and the sin of our y component to produce
noise. Using this approach, the end of our walk arrives at the same noise inputs
where we began our walk, so we get a "loopable" result!
walk_steps = 64
batch_size = 4
batches = walk_steps // batch_size
prompt = "An oil paintings of cows in a field next to a windmill in Holland"
encoding = get_text_embeddings(prompt)
walk_latent_x = random.normal((1, height // 8, width // 8, 16))
walk_latent_y = random.normal((1, height // 8, width // 8, 16))
walk_scale_x = ops.cos(ops.linspace(0.0, 2.0, walk_steps) * math.pi)
walk_scale_y = ops.sin(ops.linspace(0.0, 2.0, walk_steps) * math.pi)
latent_x = ops.tensordot(walk_scale_x, walk_latent_x, axes=0)
latent_y = ops.tensordot(walk_scale_y, walk_latent_y, axes=0)
latents = ops.add(latent_x, latent_y)
latents = ops.reshape(latents, (batches, batch_size, height // 8, width // 8, 16))
images = []
progbar = keras.utils.Progbar(batches)
for i in range(batches):
images.append(
generate_function(
latents[i],
(
ops.tile(encoding[0], (batch_size, 1, 1)),
ops.tile(encoding[1], (batch_size, 1, 1)),
ops.tile(encoding[2], (batch_size, 1)),
ops.tile(encoding[3], (batch_size, 1)),
),
ops.convert_to_tensor(num_steps),
ops.convert_to_tensor(guidance_scale),
)
)
progbar.update(i + 1, finalize=i == batches - 1)
images = ops.convert_to_numpy(decode_to_images(images, height, width))
export_as_gif(
"cows.gif",
[Image.fromarray(image) for image in images],
frames_per_second=4,
no_rubber_band=True,
)

Experiment with your own prompts and with different values of the parameters!
Conclusion
Stable Diffusion 3 offers a lot more than just single text-to-image generation. Exploring the latent manifold of the text encoder and the latent space of the diffusion model are two fun ways to experience the power of this model, and KerasHub makes it easy!